
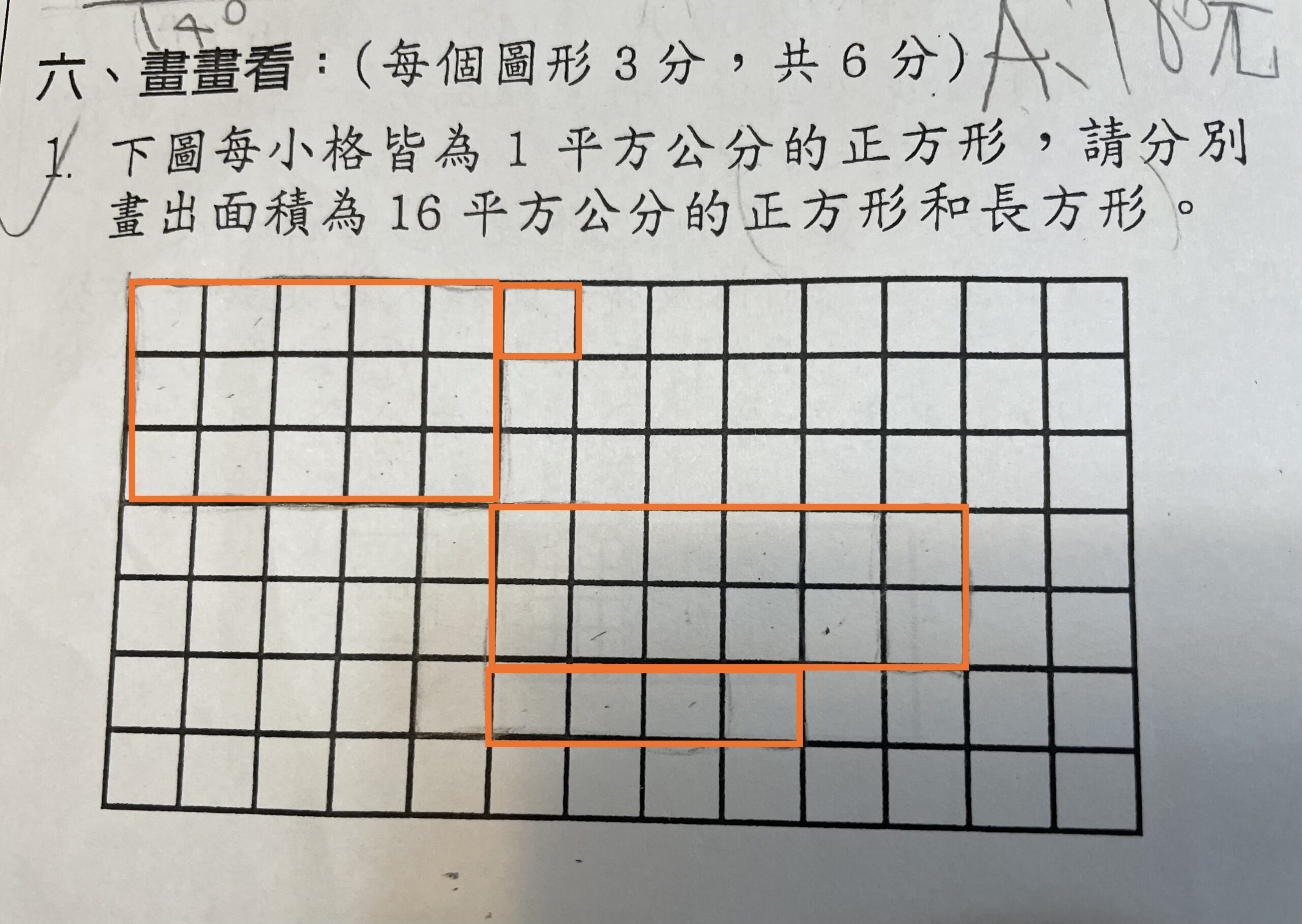
女兒在寫這種題目作業的時候,常常會畫成下圖的樣貌,讓我覺得很奇怪。我想有幾個可能性,第一個是她誤會題目的意思了,認為是要分別畫出長方形+正方形的組合,也就是題意理解的問題。第二個是,她還沒有建立乘法與平面圖形的關係,以及延伸出的面積關係。對此,我想到了兩種讓她了解的方式,第一種是我在那個當下教她的方式,第二種是我在回想的時候,突然蹦出的想法,我覺得第二種或許會更好,下次來試試。
第一種:
我先問她,她認為題目是什麼意思?她認為是要畫出「面積為16平方公分的正方形和長方形組合」,我想這部份是題目理解的問題。因此,我將「面積為16平方公分」遮住,也就是題目變為:分別畫出正方形和長方形,這時她就知道,是分別要畫出一個正方形和一個長方形。接著,再把「面積為16平方公分」打開,請她再唸一次,這次她說:「喔,是要畫一個正方形還有一個長方形,它們面積都是16平方公分嗎?」
然後,請她寫出所有積為16的乘法組合,也就是:1×16、2×8、4×4、8×2、16×1。接下來,拿出邊長為1公分的方格板與積木,請她依序排出,排好就把形狀畫出來,並著色面積的位置,如下圖所示。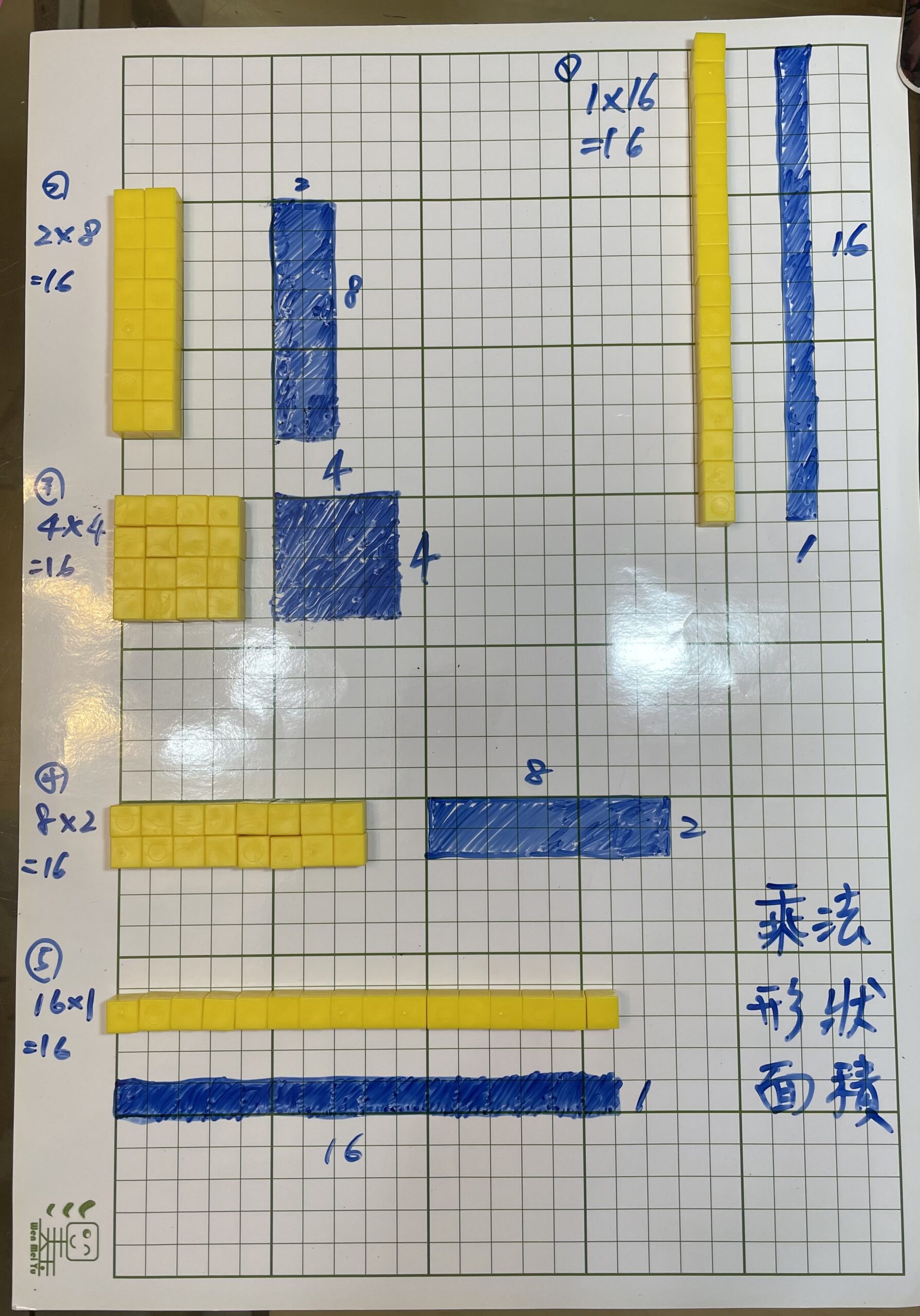
孩子發現,原來面積為16平方公分的圖形有這麼多種,而且有些是一樣的,只是直或橫的差別而已。
為了協助孩子串起乘法概念、矩形與面積三者之間的邏輯關係,以及想讓孩子知道目前所學的內容為過去學習內容的延伸,我請她先解釋數字上的乘法概念,以及數字上的乘法組合與排列出的積木的關係是什麼?例如:1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1 = 1×16,1×16表示一排有1個,總共有16排。
接著,積木可以畫成平面的長條矩形,矩形的短邊為1,長邊為16。最後,面積在哪裡?面積在矩形內部,也就是一個又一個的方格累積起來,意即一排有1個,總共有16排,因此,面積為1×16=16。它們都是在描述同一種東西,只是表示方式不同而已。
孩子懂了以後,便自己挑圖形去畫在題目格子上。
以上的做法,是在「教」,其實無形中剝奪了孩子思考的機會,也沒有辦法產生再深一層的頓悟。因此,我想下次可以用下方的方法試試,或許會更好。
第二種:
針對題目,先詢問孩子面積的概念是什麼?例如,拿出一張色紙,詢問孩子這張紙的面積在哪裡、桌子的面積在哪裡…。確認孩子懂面積的概念之後,可以在色紙上用尺畫出許多邊長為1公分的方格,讓孩子知道,面積是累積出來的。
接著,給孩子16個邊長為1公分的正方形紙片,讓她排出所有可能的正方形、長方形,依序畫成對應的矩形。最後,引導她思考,這些紙片、矩形累積的量是多少?用加法如何表示?觀察一下,是不是很長一串數字?手有沒有寫得很累?嘴有沒有唸的很痠?會不會容易搞不清楚?那有沒有更好的表示法?藉此連接到乘法概念,再請她依序用乘法表示剛剛排好的各種矩形。
這個方式的好處是,她藉由同樣的16片紙(也就是累積起來面積為16平方公分),可以自己發現原來有這麼多變化。又能自己把它變成矩形外框,產生形狀的思維。最後,有能力思考,把這些具體的紙片、平面上的方格圖形,抽象化用數字、乘法表示。
在這樣的方式裡,我是引導者的角色,而不是教學者。最重要的是,孩子在過程中練習了邏輯思考,也練習了抽象化事物的能力。我想,這是我期望孩子學數學這個學科的目的。
麗芳的眾多教案裡,有兩本數學教案,分別是數學圖形化與原來乘法算式是這樣來的,裡面以引導的方式協助孩子了解怎麼從具體的積木轉化為平面圖形與數字,還有乘法的直式運算方式、思維和矩形面積之間的關係,很有趣!
